机器学习之回归

基本数学原理

查看数据：

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 读入训练数据
train = np.loadtxt('click.csv', delimiter=',', skiprows=1)
train_x = train[:, 0]
train_y = train[:, 1]

# 绘图
plt.plot(train_x, train_y, 'o')
plt.show()

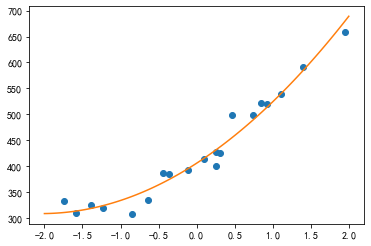
假设这是一个关于广告费与网站点击量的数据集，我们需要预测投入更多的广告费网站点击量是多少。

可以使用一条直线去拟合这个数据集：

有了这条直线，我们就可以根据新的广告费投入去预测网站点击量。

可以使用下面的函数描述这条直线：
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

注意：在统计学领域，人们常常使用 θ 来表示未知数和推测值。采用 θ加数字下标的形式，是为了防止当未知数增加时，表达式中大量出现 a、b、c、d…这的符号。这样不但不易理解，还可能会出现符号本身不够用的情况。

我们的线性回归模型目标就是求解出${\theta }_0$和${\theta }_1$两个参数。

我们得到的模型会与原始样本存在一定的误差：

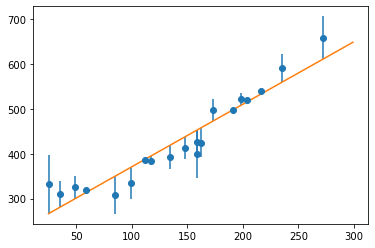
为了求解最近的θ，我们只要想办法降低样本与拟合直线的误差之和即可。描述误差之和的表达式称为目标函数E(θ)，E 是 Error 的首字母：
$$E(\theta )=\frac{1}{2}\sum _{i=1}^n{\left(y^{(i)}-f_{\theta }\left(x^{(i)}\right)\right)}^2$$
$x^{(i)}$和$y^{(i)}$指第 i 个训练数据的某个维度的值。为了找到使 E(θ) 的值最小的 θ，这样的问题称为最优化问题。

计算误差之和使用$|y-f_{\theta }(x)|$也没有错，但之后我们求解最优化问题，要对目标函数进行微分，比起绝对值，平方的微分更加简单。前面乘以1/2也和之后的微分有关系，是为了让作为结果的表达式变得简单。函数乘以正的常数，函数的形状就会被横向压扁或者纵向拉长，但函数本身取最小值的点是不变的。

为了得到最佳的θ，可以不停尝试修改参数 θ，使E(θ) 的值变得越来越小。

下面我们使用梯度下降法求解参数θ，原理：只要向与导数的符号相反的方向移动 θ， E(θ) 就会自然而然地沿着最小值的方向前进了。

对于只有一个参数x的函数g(x)有：
$$x:=x-\eta \frac{\mathrm{d}}{\mathrm{d}x}g(x)$$

A := B 这种写法的意思是通过 B 来定义 A。

η 是称为学习率的正的常数，读作“伊塔”。根据学习率的大小，到达最小值的更新次数也会发生变化，即收敛速度不同。有时候甚至会出现完全无法收敛，一直发散的情况。

比如对于函数$g(x)=(x-1{)}^2$：

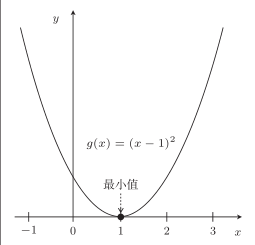
由$\frac{\mathrm{d}}{\mathrm{d}x}g(x)=2x-2$知，g(x) 的微分是 2x − 2。

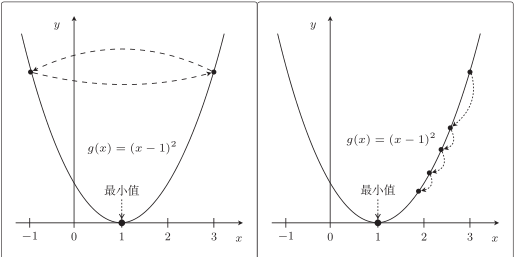
设η = 1 ，从 x = 3 开始，看看 x的变化：

x := 3 − 1(2 × 3 − 2) = 3 − 4 = −1
x := −1 − 1(2 × −1 − 2) = −1 + 4 = 3
x := 3 − 1(2 × 3 − 2) = 3 − 4 = −1

由于学习率η 过大，导致无法收敛，一直在 3 和 −1 上跳来跳去。

下面设 η = 0.1 ，同样从 x = 3 开始，再看看：

x := 3 − 0.1 × (2 × 3 − 2) = 3 − 0.4 = 2.6
x := 2.6 − 0.1 × (2 × 2.6 − 2) = 2.6 − 0.3 = 2.3
x := 2.3 − 0.1 × (2 × 2.3 − 2) = 2.3 − 0.2 = 2.1
x := 2.1 − 0.1 × (2 × 2.1 − 2) = 2.1 − 0.2 = 1.9

这次渐渐接近 x = 1 了，只是速度太慢，让人等的着急。如果 η 较大，那么 x := x − η(2x − 2) 会在两个值上跳来跳去，甚至有可能远离最小值。这就是发散状态。而当 η 较小时，移动量也变小，更新次数就会增加，但是值确实是会朝着收敛的方向而去：

而对于我们的目标函数：
$$E(\theta )=\frac{1}{2}\sum _{i=1}^n{\left(y^{(i)}-f_{\theta }\left(x^{(i)}\right)\right)}^2$$
$f_{\theta }(x)$拥有${\theta }_0$和${\theta }_1$两个参数，这个目标函数是拥有两个参数的双变量函数，所以要用偏微分。更新表达式：
$$\begin{array}{rl}{\theta }_0& :={\theta }_0-\eta \frac{\partial E}{\partial {\theta }_0}\\ {\theta }_1& :={\theta }_1-\eta \frac{\partial E}{\partial {\theta }_1}\end{array}$$
E(θ) 中有$f_{\theta }(x)$，而$f_{\theta }(x)$中又有${\theta }_0$可以使用复合函数的微分分别去考虑它们：
$$u=E(\theta )v=f_{\theta }(x)$$

$$\frac{\partial u}{\partial {\theta }_0}=\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_0}$$

先从 u 对 v 微分的地方开始计算：
$$\begin{array}{rl}\frac{\partial u}{\partial v}& =\frac{\partial }{\partial v}\left(\frac{1}{2}\sum _{i=1}^n{\left(y^{(i)}-v\right)}^2\right)\\ & =\frac{1}{2}\sum _{i=1}^n\left(\frac{\partial }{\partial v}{\left(y^{(i)}-v\right)}^2\right)\\ & =\frac{1}{2}\sum _{i=1}^n\left(\frac{\partial }{\partial v}\left(y^{(i{)}^2}-2y^{(i)}v+v^2\right)\right)\\ & =\frac{1}{2}\sum _{i=1}^n\left(-2y^{(i)}+2v\right)\\ & =\sum _{i=1}^n\left(v-y^{(i)}\right)\end{array}$$
最后一行，常数与1/2 相抵消了，微分后的表达式变简单了，这就是一开始乘以1/2 的理由。

下面是 v 对${\theta }_0$的微分：
$$\begin{array}{rl}\frac{\partial v}{\partial {\theta }_0}& =\frac{\partial }{\partial {\theta }_0}\left({\theta }_0+{\theta }_{1}x\right)\\ & =1\end{array}$$

下面将各部分相乘：
$$\begin{array}{rl}\frac{\partial u}{\partial {\theta }_0}& =\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_0}\\ & =\sum _{i=1}^n\left(v-y^{(i)}\right)\cdot 1\\ & =\sum _{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\end{array}$$
接下来再算一下对${\theta }_1$进行微分的结果：
$$\begin{array}{rl}\frac{\partial v}{\partial {\theta }_1}& =\frac{\partial }{\partial {\theta }_1}\left({\theta }_0+{\theta }_{1}x\right)\\ & =x\end{array}$$
u 对 v 微分的部分前面已经计算可以直接使用，最终对${\theta }_1$微分的结果：
$$\begin{array}{rl}\frac{\partial u}{\partial {\theta }_1}& =\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_1}\\ & =\sum _{i=1}^n\left(v-y^{(i)}\right)\cdot x^{(i)}\\ & =\sum _{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)}\end{array}$$
所以参数${\theta }_0$和${\theta }_1$的更新表达式就是这样的：
$$\begin{array}{l}{\theta }_0:={\theta }_0-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\\ {\theta }_1:={\theta }_1-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)}\end{array}$$

下面我们使用numpy实现梯度下降法求解这个问题：

梯度下降法

首先我们要实现的$f_{\theta }(x)$和目标函数$E(\theta )$
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

$$E(\theta )=\frac{1}{2}\sum _{i=1}^n{\left(y^{(i)}-f_{\theta }\left(x^{(i)}\right)\right)}^2$$

定义参数和函数：

# 参数初始化
theta0 = np.random.rand()
theta1 = np.random.rand()

# 预测函数
def f(x):
    return theta0 + theta1 * x

# 目标函数
def E(x, y):
    return 0.5 * np.sum((y - f(x)) ** 2)

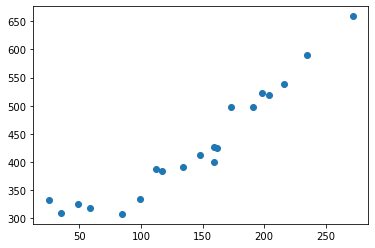
接下来为了保证参数收敛的速度不会太慢，先对训练数据进行标准化，将其变成平均值为0、方差为 1 的数据。
µ 是训练数据的平均值，σ 是标准差：
$$z^{(i)}=\frac{x^{(i)}-\mu }{\sigma }$$
python处理代码：

# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu) / sigma

train_z = standardize(train_x)
plt.plot(train_z, train_y, 'o')
plt.show()

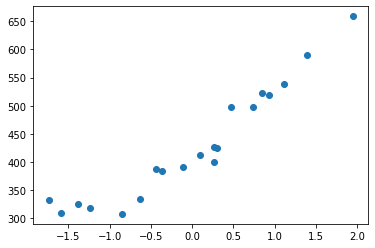
变换后的数据可以看到横轴的刻度改变了。

对于参数${\theta }_0$和${\theta }_1$的更新表达式：
$$\begin{array}{l}{\theta }_0:={\theta }_0-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\\ {\theta }_1:={\theta }_1-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)}\end{array}$$
η的值要试几次才能确定，可以先设置为$10^{-3}$尝试一下。对目标函数进行微分，不断重复参数的更新，我们可以指定重复次数，也可以比较参数更新前后目标函数的值，如果值基本没什么变化，就可以结束学习了。

numpy实现代码：

# 学习率
ETA = 1e-3

# 误差的差值
diff = 1

# 更新次数
count = 0

# 直到误差的差值小于 0.01 为止，重复参数更新
error = E(train_z, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量
    tmp_theta0 = theta0 - ETA * np.sum((f(train_z) - train_y))
    tmp_theta1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)

    # 更新参数
    theta0 = tmp_theta0
    theta1 = tmp_theta1

    # 计算与上一次误差的差值
    current_error = E(train_z, train_y)
    diff = error - current_error
    error = current_error

    # 输出日志
    count += 1
    log = '第 {} 次 : theta0 = {:.3f}, theta1 = {:.3f}, 差值 = {:.4f}'
    print(log.format(count, theta0, theta1, diff))

打印结果：

......
第 390 次 : theta0 = 428.988, theta1 = 93.444, 差值 = 0.0114
第 391 次 : theta0 = 428.991, theta1 = 93.444, 差值 = 0.0109
第 392 次 : theta0 = 428.994, theta1 = 93.445, 差值 = 0.0105
第 393 次 : theta0 = 428.997, theta1 = 93.446, 差值 = 0.0101
第 394 次 : theta0 = 429.000, theta1 = 93.446, 差值 = 0.0097

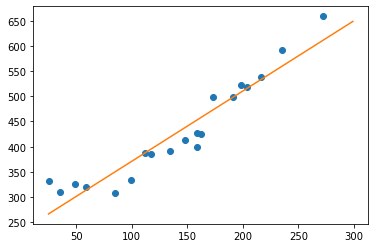
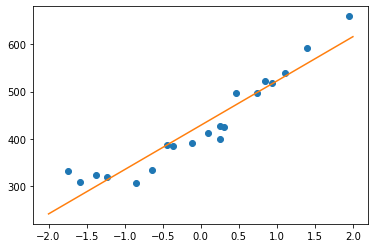
绘图查看拟合效果：

# 绘图确认
x = np.linspace(-2, 2, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(x))
plt.show()

需要预测结果时只需先将数据标准化后再传入模型中即可：

f(standardize(100))

完整代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

df = pd.read_csv("click.csv")
df.sort_values("x", inplace=True)
train = df.values
train_x = train[:, 0]
train_y = train[:, 1]

# 标准化
def standardize(x):
    mu = x.mean()
    sigma = x.std()
    return (x - mu) / sigma

train_z = standardize(train_x)

# 参数初始化
theta0 = np.random.rand()
theta1 = np.random.rand()

# 预测函数
def f(x):
    return theta0 + theta1 * x

# 目标函数
def E(x, y):
    return 0.5 * np.sum((y - f(x)) ** 2)
    
# 学习率
ETA = 1e-3

# 误差的差值
diff = 1

# 更新次数
count = 0

# 直到误差的差值小于 0.01 为止，重复参数更新
error = E(train_z, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量
    tmp_theta0 = theta0 - ETA * np.sum((f(train_z) - train_y))
    tmp_theta1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)

    # 更新参数
    theta0 = tmp_theta0
    theta1 = tmp_theta1

    # 计算与上一次误差的差值
    current_error = E(train_z, train_y)
    diff = error - current_error
    error = current_error

    # 输出日志
    count += 1
    log = '第 {} 次 : theta0 = {:.3f}, theta1 = {:.3f}, 差值 = {:.4f}'
    print(log.format(count, theta0, theta1, diff))

多项式回归

上面我们使用直线拟合了模型，但对于上面所给的数据其实曲线比直线拟合得更好：

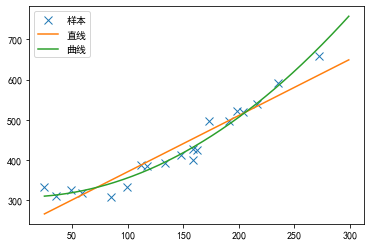
我们把$f_{\theta }(x)$定义为二次函数，就能用它来表示这条曲线了：
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$$
或者用更大次数的表达式也可以。这样就能表示更复杂的曲线了：
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+\cdots +{\theta }_n{x}^n$$
虽然次数越大拟合得越好，但难免也会出现过拟合的问题。在找出最合适的表达式之前，需要不断地去尝试。

现在我们只针对二次函数进行求解，设 u = E(θ) 、 v =$f_{\theta }(x)$，然后用 u 对${\theta }_2$偏微分，求出更新表达式。
$$\begin{array}{rl}\frac{\partial v}{\partial {\theta }_2}& =\frac{\partial }{\partial {\theta }_2}\left({\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2\right)\\ & =x^2\end{array}$$
最终更新表达式为：
$$\begin{array}{l}{\theta }_0:={\theta }_0-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\\ {\theta }_1:={\theta }_1-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)}\\ {\theta }_2:={\theta }_2-\eta {\sum }_{i=1}^n\left(f_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i{)}^2}\end{array}$$
即使再增加参数，依然可以用同样的方法求出它们的更新表达式，像这样增加函数中多项式的次数，然后再使用函数的分析方法被称为多项式回归。

将参数和训练数据都作为向量来处理，可以使计算变得更简单：
$$\mathbf{\theta }=\left[\begin{array}{l}{\theta }_0\\ {\theta }_1\\ {\theta }_2\end{array}\right]{\mathbf{x}}^{(i)}=\left[\begin{array}{c}1\\ x^{(i)}\\ x^{(i{)}^2}\end{array}\right]$$
由于训练数据有很多，我们把 1 行数据当作 1 个训练数据，以矩阵的形式来处理会更好：
$$\mathbf{X}=\left[\begin{array}{c}{\mathbf{x}}^{(1{)}^{\mathrm{T}}}\\ {\mathbf{x}}^{(2{)}^{\mathrm{T}}}\\ {\mathbf{x}}^{(3{)}^{\mathrm{T}}}\\ ⋮\\ {\mathbf{x}}^{(n{)}^{\mathrm{T}}}\end{array}\right]=\left[\begin{array}{ccc}1& x^{(1)}& x^{(1{)}^2}\\ 1& x^{(2)}& x^{(2{)}^2}\\ 1& x^{(3)}& x^{(3{)}^2}\\ & ⋮& \\ 1& x^{(n)}& x^{(n{)}^2}\end{array}\right]$$
再求这个矩阵与参数向量 θ 的积：
$$\mathbf{X}\mathbf{\theta }=\left[\begin{array}{ccc}1& x^{(1)}& x^{(1{)}^2}\\ 1& x^{(2)}& x^{(2{)}^2}\\ 1& x^{(3)}& x^{(3{)}^2}\\ & ⋮& \\ 1& x^{(n)}& x^{(n{)}^2}\end{array}\right]\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{c}{\theta }_0+{\theta }_1{x}^{(1)}+{\theta }_2{x}^{(1{)}^2}\\ {\theta }_0+{\theta }_1{x}^{(2)}+{\theta }_2{x}^{(2{)}^2}\\ ⋮\\ {\theta }_0+{\theta }_1{x}^{(n)}+{\theta }_2{x}^{(n{)}^2}\end{array}\right]$$
python描述代码：

# 参数初始化
theta = np.random.rand(3)

# 创建训练数据的矩阵
def to_matrix(x):
    return np.vstack([np.ones(x.size), x, x ** 2]).T

X = to_matrix(train_z)

# 预测函数
def f(x):
    return np.dot(x, theta)

更新表达式可以写成通用的表达式：
$${\theta }_j:={\theta }_j-\eta \sum _{i=1}^n\left(f_{\theta }\left({\mathbf{x}}^{(i)}\right)-y^{(i)}\right)x_j^{(i)}$$
这时我们好好利用训练矩阵X，就能一下子全部计算出来。在 j = 0 的时，设：
$$f=\left[\begin{array}{c}{f}_{\theta }\left({\mathbf{x}}^{(1)}\right)-y^{(1)}\\ f_{\theta }\left({\mathbf{x}}^{(2)}\right)-y^{(2)}\\ ⋮\\ f_{\mathbf{\theta }}\left({\mathbf{x}}^{(n)}\right)-y^{(n)}\end{array}\right]{\mathbf{x}}_0=\left[\begin{array}{c}{x}_0^{(1)}\\ x_0^{(2)}\\ ⋮\\ x_0^{(n)}\end{array}\right]$$
则：
$$\sum _{i=1}^n\left(f_{\theta }\left({\mathbf{x}}^{(i)}\right)-y^{(i)}\right)x_0^{(i)}={\mathbf{f}}^{\mathrm{T}}{\mathbf{x}}_0$$
这里考虑的还只是 j = 0 的情况，而参数共有 3 个，再用同样的思路考虑$x_1$和$x_2$的情况就好了。
$$\begin{array}{l}{x}_0=\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right],x_1=\left[\begin{array}{c}{x}^{(1)}\\ x^{(2)}\\ ⋮\\ x^{(n)}\end{array}\right],x_2=\left[\begin{array}{c}{x}^{(1{)}^2}\\ x^{(2{)}^2}\\ ⋮\\ x^{(n{)}^2}\end{array}\right]\\ X=\left[\begin{array}{lll}{x}_0& x_1& x_2\end{array}\right]=\left[\begin{array}{ccc}1& x^{(1)}& x^{(1{)}^2}\\ 1& x^{(2)}& x^{(2{)}^2}\\ 1& x^{(3)}& x^{(3{)}^2}\\ ⋮& & \\ 1& x^{(n)}& x^{(n{)}^2}\end{array}\right]\end{array}$$
最后该将 f 和这个 X 相乘就可以了：
$${\mathbf{f}}^{\mathrm{T}}\mathbf{X}$$
python语言描述：

# 误差的差值
diff = 1

# 更新次数
count = 0

# 直到误差的差值小于 0.01 为止，重复参数更新
error = E(X, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量
    theta = theta - ETA * np.dot(f(X) - train_y, X)

    # 计算与上一次误差的差值
    current_error = E(X, train_y)
    diff = error - current_error
    error = current_error

完整代码：

import numpy as np
import matplotlib.pyplot as plt

# 读入训练数据
train = np.loadtxt('click.csv', delimiter=',', dtype='int', skiprows=1)
train_x = train[:,0]
train_y = train[:,1]

# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu) / sigma

train_z = standardize(train_x)

# 参数初始化
theta = np.random.rand(3)

# 创建训练数据的矩阵
def to_matrix(x):
    return np.vstack([np.ones(x.size), x, x ** 2]).T

X = to_matrix(train_z)

# 预测函数
def f(x):
    return np.dot(x, theta)

# 目标函数
def E(x, y):
    return 0.5 * np.sum((y - f(x)) ** 2)

# 学习率
ETA = 1e-3

# 误差的差值
diff = 1

# 更新次数
count = 0

# 直到误差的差值小于 0.01 为止，重复参数更新
error = E(X, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量
    theta = theta - ETA * np.dot(f(X) - train_y, X)

    # 计算与上一次误差的差值
    current_error = E(X, train_y)
    diff = error - current_error
    error = current_error

    # 输出日志
    count += 1
    log = '第 {} 次 : theta = {}, 差值 = {:.4f}'
    print(log.format(count, theta, diff))

# 绘图确认
x = np.linspace(-2, 2, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(to_matrix(x)))
plt.show()