原文发表于:

top-K问题是很常见的。在T公司的两次面试中,都遇到了这个问题,在S公司的面试中,也遇到了这个问题。本文来具体聊一下top-K问题:有N个整数,求出最大的K个值,内存无法容纳这N个整数。

一眼便知道是海量数据问题,直接用堆就行了,确实如此。但是,我觉得这样太经验主义了,为什么要用堆呢?为什么不用其它的数据结构呢?
我们来简化一下上面的题目:
有N个整数,求出最大的K个值,其中K=1,内存可以容纳这N个整数。
求最大值,就跟擂台赛差不多,姑且认为最开始上台的人是最强的,然后第二个上场,败者被淘汰,胜者继续留在台上。最后,留在台上的人就是最强的。

求最大值代码如下,简单得很:
package main
import "fmt"
func findMax(a []int) int {
max := a[0] // 假设a的长度大于0
for _, v := range a {
if v > max { // 擂台赛,新来的v胜利了,要留在台上
max = v
}
}
return max
}
func main() {
a := []int{3, 4, 2, 1, 9, 5, -1, 18, 6}
fmt.Println(findMax(a))
}
下面,我们来看top-K问题, 很显然,可以采用类似的思路:随便找出K个值,认为它们是最大的K个值,然后遍历其它元素v,如果v比K个值的最小值还小,则v没有资格成为最大的K个值;如果v比K个值的最小元素要大,则这个最小值没有资格成为最大K个值中的一员,需要被v替代,原理和擂台赛相似。
那么,怎么找出K个元素的最小值呢?显然,小顶堆是非常适合的。我们来看下小顶堆的定义:
(1)小顶堆每个结点的值,不小于其父结点的值;
(2)小顶堆是一棵完全二叉树。
小顶堆的数据结构如下:
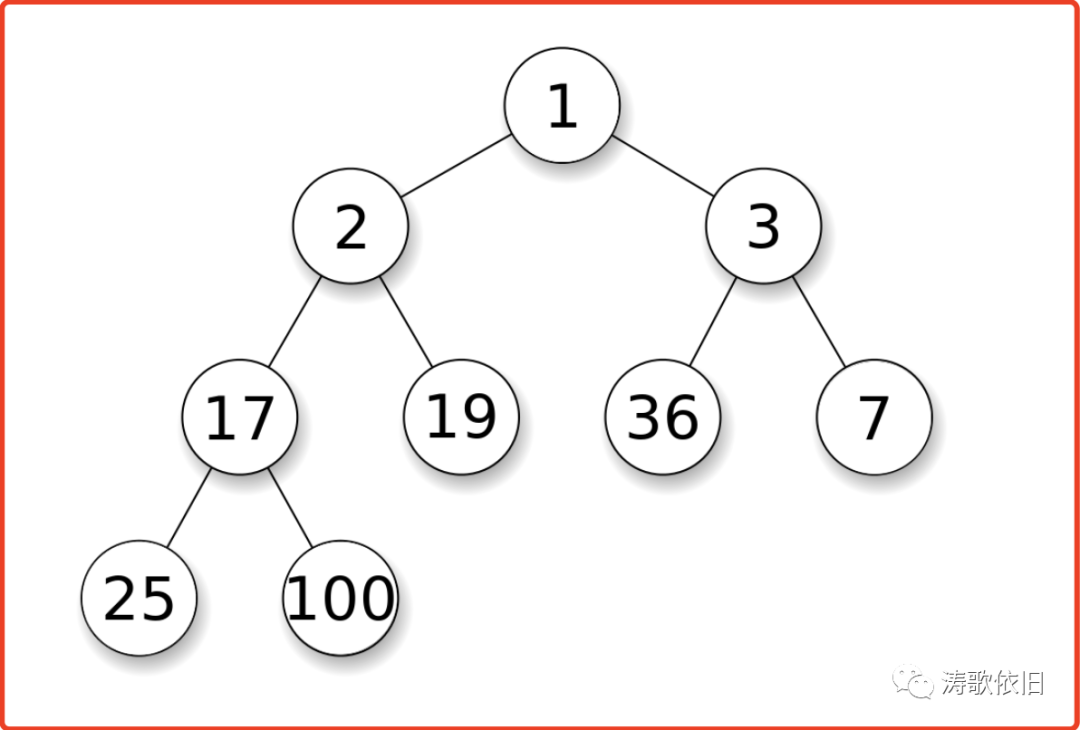
怎么去实现一个堆呢?堆是一颗完全二叉树,非常紧凑,所以用数组来存储是比较方便的。关于堆的代码,本文就不再单独列出来了。
在笔试面试的时候,如果能写出堆的代码,当然很好。如果实在写不出来,也要跟面试官讲清楚自己的思路,毕竟思路是非常重要的。
堆是一种很美的数据结构,堆的另外一个应用是堆排序,有兴趣的朋友可以查阅相关资料,进行深入了解。