Biegral Blog

题目描述：

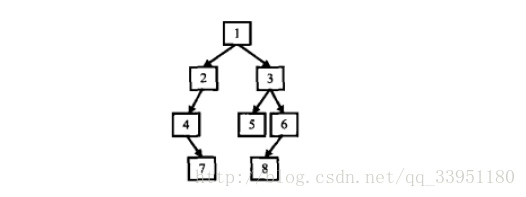
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历结果中都不含重复的数字。例如输入前序遍历序列｛1,2,4,7,3,5,6,8｝和中序遍历序列｛4,7,2,1,5,3,8,6｝，则重建出如图所示的二叉树并输出它的头结点。

分析及实现：

• 思路分析
  根据二叉树前序遍历的特点（根-左-右），每次读取的第一个值一定是根节点，这样我们可以在中序遍历的序列中找到当前的根节点的位置。
  根据中序遍历的特点（左-根-右），当确定了一个根节点后，其左边序列就是这个根节点的左子树，右边序列就是其右子树。
  
  如此看来，我们每次都需要在前序遍历中找根节点并创建一个根节点，然后在中序遍历中确定根节点位置，并确定当前根节点的左右子树，然后以同样的方法去构建左右子树。这整个过程其实是一个递归的过程。

• 代码实现
  在实现的时候，我们需要每次记录根节点的左右序列值，以便下一次找根节点构建树，因此这里使用vector来记录

//根据前序遍历和中序遍历重建二叉树
Node* RebuildTree(vector<int> prev, vector<int> vin)
{
    if (prev.empty() || vin.empty())
        return NULL;

    //在前序遍历中prev中找根节点，并确定其在vin的位置
    size_t index = 0;
    for (; index<vin.size(); index++)
    {
        if (vin[index] == prev[0])
            break;
    }
    //已经找到根节点，并构造根节点
    Node* root = new Node(prev[0]);
    //Print(root);
    //根据中序遍历将根节点左右两侧一分为二，根节点的左侧为左子树，右侧为右子树
    vector<int> prev_left,prev_right;
    vector<int> vin_left,vin_right;
    //先将前序、中序中根节点的左右子树记录下来
    for (size_t j=0; j<index; j++)
    {
        prev_left.push_back(prev[j+1]);
        vin_left.push_back(vin[j]);
    }
    for (size_t j=index+1; j<vin.size(); j++)
    {
        prev_right.push_back(prev[j]);
        vin_right.push_back(vin[j]);
    }
    //递归构造左右子树
    root->_left = RebuildTree(prev_left,vin_left);
    root->_right = RebuildTree(prev_right,vin_right);

    return root;
}