直接选择排序和堆排序都属于选择排序
ps:仍以升序为例!
一、直接选择排序
直接选择排序的思想:
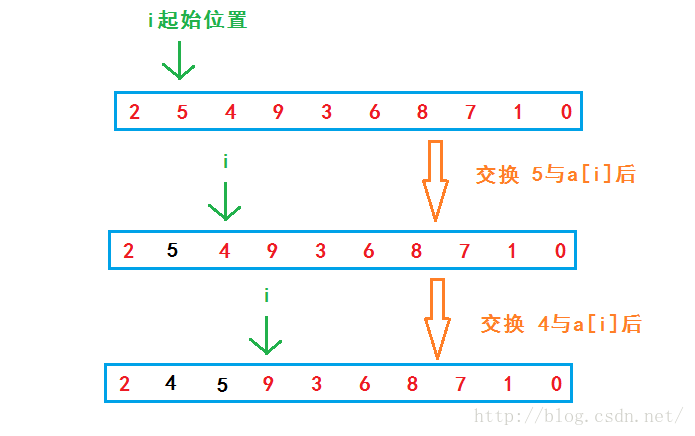
选择排序就是通过n-i次关键字的比较,每次从n-i+1个记录中找出最小的关键字,将其与第i个位置的数据交换。
void SelectSort(int* a, size_t size)
{
assert(a);
int max = 0;
for (size_t i=0; i<size; ++i)
{
max = i;
for (size_t j=i+1; j<size; ++j)
{
if (a[j] > a[max])
{
max = j;
}
}
if (i != max)
swap(a[i],a[max]);
}
}
直接选择排序的优化:
上边简单的选择排序是每次选出一个数来交换,优化后的做法是从数组的两边开始遍历,每次选出一个最大的数一个最小的数来进行交换
void SelectSort(int* a,int size)
{
assert(a);
int left = 0;
int right = size-1;
while(left < right)
{
int min = left;
int max = left;
//在[left,right]区间内找最大最小
for (int i=left; i<=right; ++i)
{
if (a[i] < a[min])
min = i; //找到[left,right]内最小值的下标
if (a[i] > a[max])
max = i; //找到[left,right]内最大值的下标
}
swap(a[left],a[min]); //将最小值放在区间最左边
if (left == max)
{
max = min; //更换max的位置
}
swap(a[right],a[max]); //将最大值放在区间最右边
++left;
--right;
}
}最好的情况下,时间复杂度为O(0),最坏的情况是当数组逆序或接近于逆序时,此时共需要比较n-1 + n-2 + ......,其结果也是O(N^2)
二、堆排序
堆排序是利用建堆来进行排序的一种算法。
堆排序的思想:
(假若要得到的数组排序以后是升序的)先建大堆,每次取出堆顶的数据与堆数组的末尾元素进行交换,然后再接着向下调整使其重新成为一个大堆,然后再重复上面的工作,这样就可以得到一个有序的数组。需要提醒的是:每次交换完数据以后,只需要对size-1个数据进行调整,也就是已经在堆数组末尾的元素不进堆,这样才能得到结果!
之前写了堆排序的代码,在这篇文章里:《堆排序算法》
堆排序的时间复杂度:
我们比较的时候是从倒数第一个非叶子结点开始向前遍历的,并将其与孩子结点进行比较和交换,对于每一个非叶子节点来说,我们最多需要比较和交换两次,因此建堆时的时间复杂度是O(N)。
进行排序时,每次取堆顶数据时的实践复杂度为O(logN)(longN是以2为底N的对数),总共需要取N-1次堆顶数据进行重建堆,因此时间复杂度为O(N*logN)。
因此,堆排序的时间复杂度为O(N*logN)
三、冒泡排序
冒泡排序是我们开始编程接触的第一个排序算法,这里我就不详细写了,之前写了一篇博客:《冒泡排序及其优化》,这里边有一般的冒泡排序,以及优化以后的。
冒泡排序的时间复杂度:
最好的情况是数组数据接近于有序或其本身就是有序的,时间复杂度为O(N),最坏的情况是逆序,冒泡排序需要比较和移动的次数是1+2+3+.....+(n-1),其时间复杂度为O(N^2)。因此,冒泡排序的时间复杂度为O(N^2)。
冒泡排序与插入排序的比较:
冒泡排序虽然简单,其时间复杂度与插入排序也是一样的,这样看不出什么差别,但当数据比较多时,冒泡排序就要比插入排序差一些,比如当有N个(若N=1万)数据:1,2,3....,9,7......这组数据是有序的,利用插入排序只需要多比较2次,但如果用冒泡排序,首先会遍历一遍(N次),接着交换完成后,需要再遍历一遍(N次)检查是否需要有数据继续交换。