超级详细的二叉树的3种遍历方法的递归和非递归的实现

Biegral 2018/3/4 22:24:11 915

二叉树是一种非常重要的数据结构，很多的数据结构都是基于二叉树的基础演变过来的。二叉树的前，中， 后3种遍历方式，因为树的定义本身就是递归定义的，所以采用递归的方法来实现是很简单的。递归开销会很大，如果使用非递归的方式需要用到栈来进行模拟，递归本身也是建立在栈的基础上的。下面将详细介绍这3种方式的递归实现和非递归实现。（非递归遍历是面试笔试的重点！！！比较的详细（啰嗦。。。。））

一：先序遍历（递归）（简单介绍）
   
  1. void pre_traverse(BTree pTree)  
  2. {  
  3.     if(pTree)  
  4.     {  
  5.         printf("%c ",pTree->data);  
  6.         if(pTree->pLchild)  
  7.             pre_traverse(pTree->pLchild);  
  8.         if(pTree->pRchild)  
  9.             pre_traverse(pTree->pRchild);      
  10.     }  
  11. }  

二：中序遍历（递归）
  1. void in_traverse(BTree pTree)  
  2. {  
  3.     if(pTree)  
  4.     {  
  5.         if(pTree->pLchild)  
  6.             in_traverse(pTree->pLchild);  
  7.         printf("%c ",pTree->data);  
  8.         if(pTree->pRchild)  
  9.             in_traverse(pTree->pRchild);   
  10.     }  
  11. }  

三：后序遍历（递归）
 
  1. void beh_traverse(BTree pTree)  
  2. {  
  3.     if(pTree)  
  4.     {  
  5.         if(pTree->pLchild)  
  6.             beh_traverse(pTree->pLchild);  
  7.         if(pTree->pRchild)  
  8.             beh_traverse(pTree->pRchild);      
  9.         printf("%c ",pTree->data);  
  10. }  

总结：三种递归的遍历方法，先序， 中序， 后序在程序的实现上对应的是打印节点数据的语句的位置。

四：先序遍历的非递归实现（详细说明）
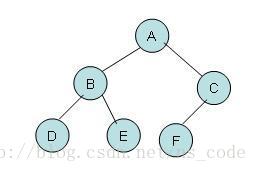
       根， 左， 右 ，一定得明白整个遍历的顺序！所以先序遍历的结果应该为：ABDECF

                                              超级详细的二叉树的3种遍历方法的递归和非递归的实现
    思路分析：首先根据一颗简单的二叉树，将整个先序遍历的过程顺一遍，当然这得借助于栈因为需要回退。
    首先找到根节点A设为当前结点，进行打印输出，然后进行压栈，然后将其左孩子B设置为当前结点。如果B不为空，则打印输出B，压栈，找到其左孩子D，D不为空，打印，压栈，并找到其左孩子设置为当前结点。（其实很明显，上面有明显的重复操作就是：结点不为空，打印， 压栈，找到其左孩子并且将其设置为当前结点！）
    这时D的左孩子为空了，应该怎么办？按照根， 左， 右很自然的想到找D的右孩子呗，要想找到D的右孩子必然得通过D，此时的当前结点已经被我们设置为D的左结点了，所以在找其右结点之前需要将D结点从栈中弹出来获得，然后在将当前操作结点设置为D的右结点。总结为：当前左孩子为空，则进行栈弹出，获得栈顶，然后将当前结点设置为其右孩子。
    当前结点为D的右孩子，为空，根据先序遍历的结果，下一个应该是E，那是如何得到的呢？想要获得E，E为B结点的右孩子，所以先找到B结点，B结点是当前栈顶元素，所以我们直接进行出栈，获取栈顶，将当前结点设置为其右结点E。总结为：当前右孩子为空，则进行栈弹出，获得栈顶，然后将当前结点设置为其右孩子。
    （下面同理可以知道，操作如下：）
    当前结点E不为空，则打印，输出，压栈，当前结点设置为其左孩子。
    当前结点E的左孩子为空，则出栈，取栈顶E，将其右孩子设置为当前结点。
    当前结点E的右孩子为空，则出栈，取栈顶A，将其右孩子设置为当前结点。
    当前结点为C不为空，则打印，输出，压栈，并将其左孩子设置为当前结点。
    当前结点C的左孩子F不为空，则打印输出，压栈，并将其左孩子设置为当前结点。
    当前结点F的左孩子为空，则弹出，取栈顶F，将其右孩子设置为当前结点。
    当前结点F的右孩子为空，则弹出，取栈顶C，将其右孩子设置为当前结点。
    当前结点C的右孩子为空，则弹出，取栈顶A，注意此时栈空了，并且当前的结点为空，则遍历结束了！

   
    整个过程顺下来，是不是感觉很清晰了，有规律性！总共3部分：根，左，右
    根：结点进行打印，输出，并压栈，将其左孩子设置为当前结点
    左：左结点不为空就执行上面根一样的操作，如果为空，则进行栈的弹出，取栈顶，将当前结点设置为其右孩子
   右：右结点不为空就执行上面根一样的操作，如果为空，则进行栈的弹出，取栈顶，将当前结点设置为其右孩子
   
    那么代码应该如何组织呢？首先不论进入整棵树，还是左子树，右子树，都会有自己的根，所以根操作是必须，不可少的。然后观察左，右会发现两者一样的操作，可以设计为一个循环，对于当前结点一样的操作。为：
     根：结点进行打印，输出，并压栈，将其左孩子设置为当前结点
     当前结点不为空就执行上面根一样的操作，如果为空，则进行栈的弹出，取栈顶，将当前结点设置为其右孩子

则具体实现代码如下：
 
  1. void pre_traverse(BTree pTree)  
  2. {  
  3.     PSTACK stack = create_stack();  //创建一个空栈  
  4.     BTree node_pop;                 //用来保存出栈节点  
  5.     BTree pCur = pTree;             //定义用来指向当前访问的节点的指针  
  6.   
  7.     //直到当前节点pCur为NULL且栈空时，循环结束  
  8.     while(pCur || !is_empty(stack))  
  9.     {  
  10.         //从根节点开始，输出当前节点，并将其入栈，  
  11.         //同时置其左孩子为当前节点，直至其没有左孩子，及当前节点为NULL  
  12.         printf("%c ", pCur->data);  
  13.         push_stack(stack,pCur);  
  14.         pCur = pCur->pLchild;  
  15.         //如果当前节点pCur为NULL且栈不空，则将栈顶节点出栈，  
  16.         //同时置其右孩子为当前节点,循环判断，直至pCur不为空  
  17.         while(!pCur && !is_empty(stack))  
  18.         {  
  19.             pCur = getTop(stack);  
  20.             pop_stack(stack,&node_pop);  
  21.             pCur = pCur->pRchild;              
  22.         }  
  23.     }  
  24. }  
    
五：中序遍历非递归
    根据中序遍历的顺序：先是左子树，然后是根，最后是右子树；每个子树的遍历都是按照这种顺序来进行处理的。根据图中分析结果为：DBEAFC
    
                                                      超级详细的二叉树的3种遍历方法的递归和非递归的实现
非递归思路如下：
     对于任意的结点P：
  1.     若P的左孩子不为空，则将其入栈，当前结点指向其左孩子；然后对当前结点进行相同的处理，知道左孩子为空；
  2. 当前结点的左孩子为空，则找到最左边的结点了，那么就将当前结点输出并打印，然后将当前结点指向其右结点，
  3. 如果其右结点不为空，就按照1， 2的步骤重复进行。
  4. 如果当前的右结点为空了，那么就出栈，并打印出栈结点，并将出栈结点的右结点设为当前结点。判断其空或者不空，重复执行3， 4操作
  5. 直到当前结点为空并且栈为空时，遍历结束！
下面通过该图来具体的顺一遍过程：
     1：当前结点P为A， 先看其左孩子有吗？有则将P压栈，并且将P重新指向A的左孩子B，然后看B的左孩子D，将B压栈，P指向D，然后看D有左孩子吗？D没有，那么根据左，根，右的顺序：打印根D结点，然后将当前结点指向其右孩子进行处理。
     2：其右孩子为空，则该小子树的左，根，右都结束了，需要回退到上一层，进行出栈获得结点B为当前结点。二B结点的左孩子刚刚已经处理了，所以直接将其输出，并将当前结点设置为其右结点E。
     3：E的左孩子没有，则直接打印E，并将其右结点设置为其当前结点。为空则继续出栈获得A。
     4：打印A：此时已经打印了：DBEA。然后将当前结点设置为其右结点C，然后看其是否有左孩子。
     5:有，则将C压栈，当前结点设置为其左孩子F，然后看F是否有左孩子，没有则打印该结点，并且当前结点设置为其右孩子。DBEAF
     6：当前结点为空，则出栈获得结点C，进行打印输出，并将其右结点设为当前结点，为空则出栈打印，此时栈空了。DBEAFC
    7：栈空并且当前结点为空时，则遍历结束：DBEAFC

    总结：
    1：每棵树进去第一件事看当前结点是否有左孩子，有则压栈，当前结点移动到其左孩子；无则打印，并且将其右结点设为当前结点。
    2：右结点不为空，重复1的操作，为空则进行出栈，打印栈顶结点，并且将栈顶结点的右孩子设置为当前结点。重复2，右结点的操作。

   代码该如何设计呢？栈空并且当前结点为空时，则遍历结束，所以会有一个总遍历的主循环；循环体中：首先先判断是否有左孩子，有则压栈，当前结点移动到其左孩子；无则打印，并且将其右结点设为当前结点。
   对于右孩子其中如果不为空，重复上面左，根，右操作，等于进入一个新树，所以就进入下一个循环了。
   对于右孩子为空则要单独处理：进行出栈，打印栈顶结点，并且将栈顶结点的右孩子设置为当前结点。新的右孩子也要进行判断为空与否，为空也要进行刚刚的操作，所以需要设计成一个循环。次循环
   所以一个主循环体，判断条件是栈空并且当前结点为空时结束；一个次循环，循环条件就是右结点是否为空。

具体代码实现：
  1. void in_traverse(BTree pTree)  
  2. {  
  3.     PSTACK stack = create_stack();  //创建一个空栈  
  4.     BTree node_pop;                 //用来保存出栈节点  
  5.     BTree pCur = pTree;             //定义指向当前访问的节点的指针  
  6.   
  7.     //直到当前节点pCur为NULL且栈空时，循环结束  
  8.     while(pCur || !is_empty(stack))  
  9.     {  
  10.         if(pCur->pLchild)  
  11.         {  
  12.             //如果pCur的左孩子不为空，则将其入栈，并置其左孩子为当前节点  
  13.             push_stack(stack,pCur);  
  14.             pCur = pCur->pLchild;  
  15.         }  
  16.         else  
  17.         {  
  18.             //如果pCur的左孩子为空，则输出pCur节点，并将其右孩子设为当前节点，看其是否为空  
  19.             printf("%c ", pCur->data);  
  20.             pCur = pCur->pRchild;  
  21.             //如果为空，且栈不空，则将栈顶节点出栈，并输出该节点，  
  22.             //同时将它的右孩子设为当前节点，继续判断，直到当前节点不为空  
  23.             while(!pCur && !is_empty(stack))  
  24.             {  
  25.                 pCur = getTop(stack);  
  26.                 printf("%c ",pCur->data);      
  27.                 pop_stack(stack,&node_pop);  
  28.                 pCur = pCur->pRchild;  
  29.             }  
  30.         }  
  31.     }  
  32. }  

六：后序遍历非递归
     后序：左， 右， 根：则后序遍历的结果应为：DEBFCA
                                                  超级详细的二叉树的3种遍历方法的递归和非递归的实现
    分析：
    首先进行顺一遍遍历的顺序：从A进入，左孩子存在，到B，B的左孩子也存在，到D，D没有左孩子了，那么他就是最左的那个了，根据左，右， 根在这个DBE子树中右结点是E结点，然后他也没有左孩子也没有右孩子所以直接打印输出E，然后输出B，其中BDE在这棵大树中属于左的范围，在根据左，右， 根，所以下一步应该着手CF这棵右子树了，到达C然后C有左孩子，进入到F，F没有左孩子也没有右孩子，所以打印输出，回退到C，打印，在回退到A。最终遍历的结果为：DEBFCA

    关键！！！回退的顺序需要栈来进行帮忙：出栈为左，右，根，则压栈顺序应该为根，右，左！

   总结一下思路：（普及到每个结点）
    1）对于任意个结点P，首先需要将其入栈
    2）如果P没有左孩子也没有右孩子，或者有左孩子或者右孩子，但是左右孩子已经被输出了，那么就可以把该结点直接进行输出，并将其出栈，将出栈的结点定义为上一个结点，并把当前栈顶的元素重新置为当前结点。
    3）如果不满足2）的条件，则将其右孩子左孩子入栈。当前结点重新置为栈顶结点，然后重复2）
    4）直至栈顶为空，然后遍历结束。
         
    设计思路：
    首先：设置两个指针：cur指向当前栈顶的结点，为当前结点；pre则指向上一个访问的结点。
    1）cur首先指向根结点，pre为空，将根压栈；由于A结点既有左孩子又有右孩子所以将其右孩子，左孩子依次压栈，然后更新cur为B；
    2）由于B结点既有左孩子又有右孩子所以将其右孩子，左孩子依次压栈，然后更新cur为D；
    3）由于D结点既没有左孩子又没有右孩子，所以直接将其出栈输出D，并更新cur为E， pre 为D；
    4）由于E结点既没有左孩子又没有右孩子，所以直接将其出栈输出E，并更新cur为B， pre 为E；
    5)  由于B结点有左右孩子但是都已经输出了，所以输出B，出栈，然后更新cur为C， pre 为B;
    6)  由于C结点右左孩子，则将左孩子入栈，然后更新cur为F， pre 为B;
    7)  由于F结点既没有左孩子又没有右孩子，所以直接将其出栈输出F，并更新cur为C， pre 为F；
    8)  由于C结点有左孩子但是都已经输出了，所以输出C，出栈，然后更新cur为A， pre 为C;
    9)  由于A结点有左右孩子但是都已经输出了，所以输出A，出栈，然后更新cur为NULL， pre 为A;
    10）栈空，则遍历结束：

具体实现代码：
   
  1. void beh_traverse(BTree pTree)  
  2. {  
  3.     PSTACK stack = create_stack();  //创建一个空栈  
  4.     BTree node_pop;          //用来保存出栈的节点  
  5.     BTree pCur;              //定义指针，指向当前节点  
  6.     BTree pPre = NULL;       //定义指针，指向上一各访问的节点  
  7.   
  8.     //先将树的根节点入栈  
  9.     push_stack(stack,pTree);    
  10.     //直到栈空时，结束循环  
  11.     while(!is_empty(stack))  
  12.     {  
  13.         pCur = getTop(stack);   //当前节点置为栈顶节点  
  14.         if((pCur->pLchild==NULL && pCur->pRchild==NULL) ||   
  15.             (pPre!=NULL && (pCur->pLchild==pPre || pCur->pRchild==pPre)))  
  16.         {  
  17.             //如果当前节点没有左右孩子，或者有左孩子或有孩子，但已经被访问输出，  
  18.             //则直接输出该节点，将其出栈，将其设为上一个访问的节点  
  19.             printf("%c ", pCur->data);  
  20.             pop_stack(stack,&node_pop);  
  21.             pPre = pCur;  
  22.         }  
  23.         else  
  24.         {  
  25.             //如果不满足上面两种情况,则将其右孩子左孩子依次入栈  
  26.             if(pCur->pRchild != NULL)  
  27.                 push_stack(stack,pCur->pRchild);  
  28.             if(pCur->pLchild != NULL)  
  29.                 push_stack(stack,pCur->pLchild);  
  30.         }  
  31.     }  
  32. }
    
本文转载:CSDN博客

阅读排行

分类

归档